卷积核kernel、滤波器filter、层layer的概念区别
本文最后更新于:2024年3月18日 下午
在单通道版本中,卷积核和滤波器两者等价。滤波器相当于是卷积核的一个集合。
单通道版本
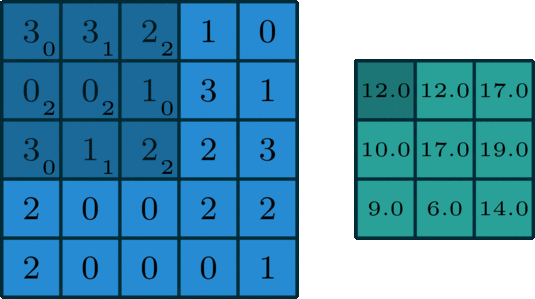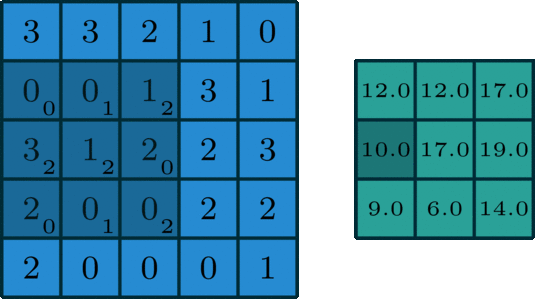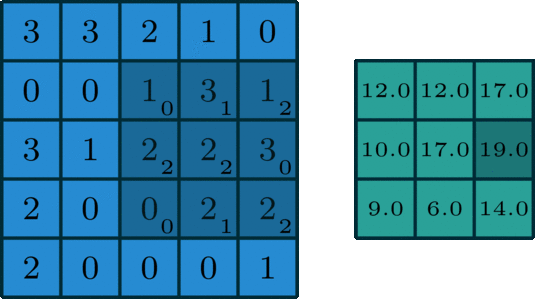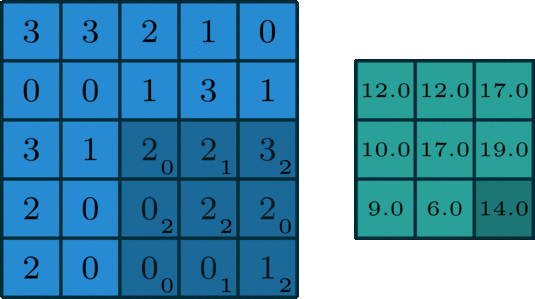
如上图所示,卷积是元素对元素的加法和乘法。这里的滤波器是一个 3*3 的矩阵[[0, 1, 2], [2, 2, 0], [0, 1, 2]],滤波器滑过输入,在每个位置完成一次卷积,得到一个数值,最终输出仍是一个 3*3 的矩阵。这里滑动的可以说是卷积核,也可以说是滤波器,两者在单通道时等价,此时的滤波器就是只有一个卷积核的集合。
多通道版本
此处介绍一些术语,层 - layer,channel - 通道,feature map - 特征图,filter - 滤波器,kernel - 卷积核。在这里通道和特征图是同一个意思,一层可以有多个通道(也可以说有多个特征图)如果输入的是一个 RGB 图像,那么就有 3 个通道。
”channel“ 是通常被用来描述 ”layer“ 的结构,相似的,”kernel“ 是通常被用来描述 ”filter“ 的结构,layer 和一个个 ”channel“ 堆叠而成,”filter“ 则是一个个 ”kernel“ 堆叠而成。一个 ”kernel“ 更倾向于是 2D 的权重矩阵,而 ”filter“ 则是多个 ”kernel“ 堆叠的 3D 结构。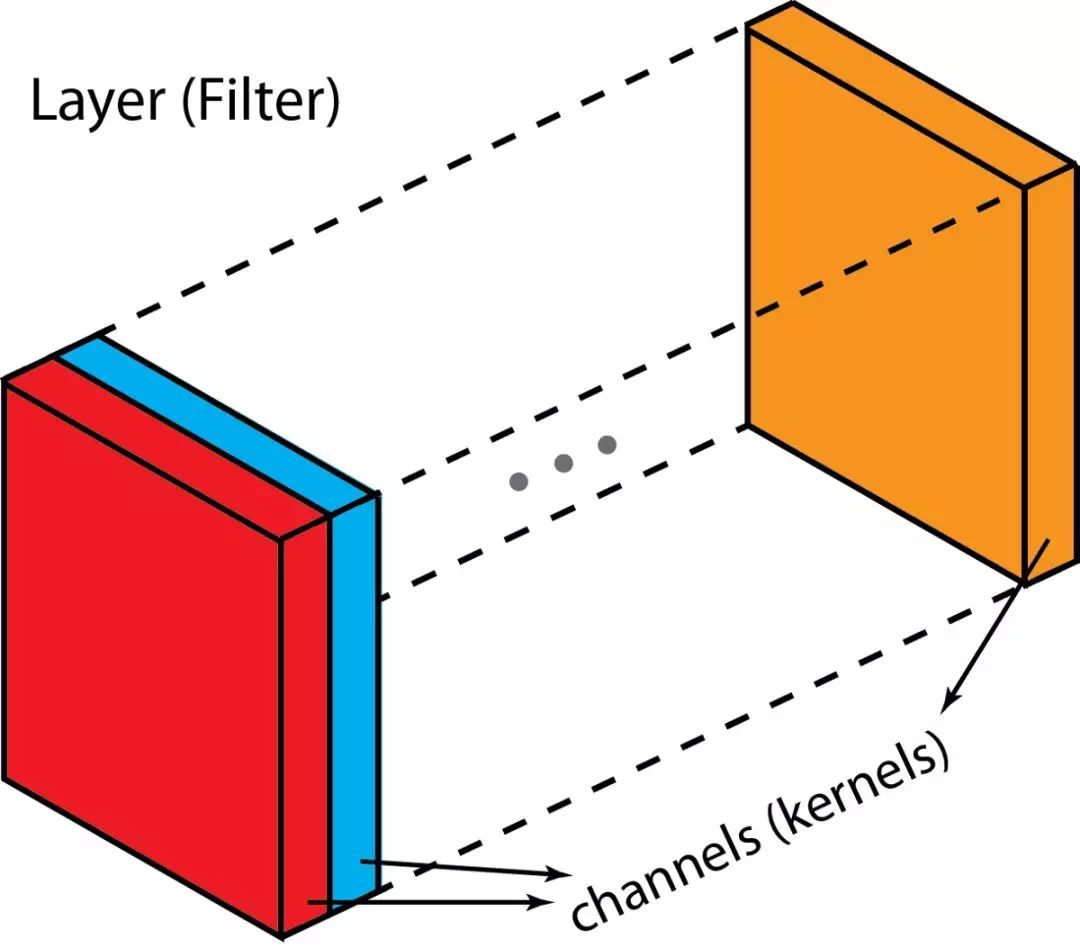
2D 卷积
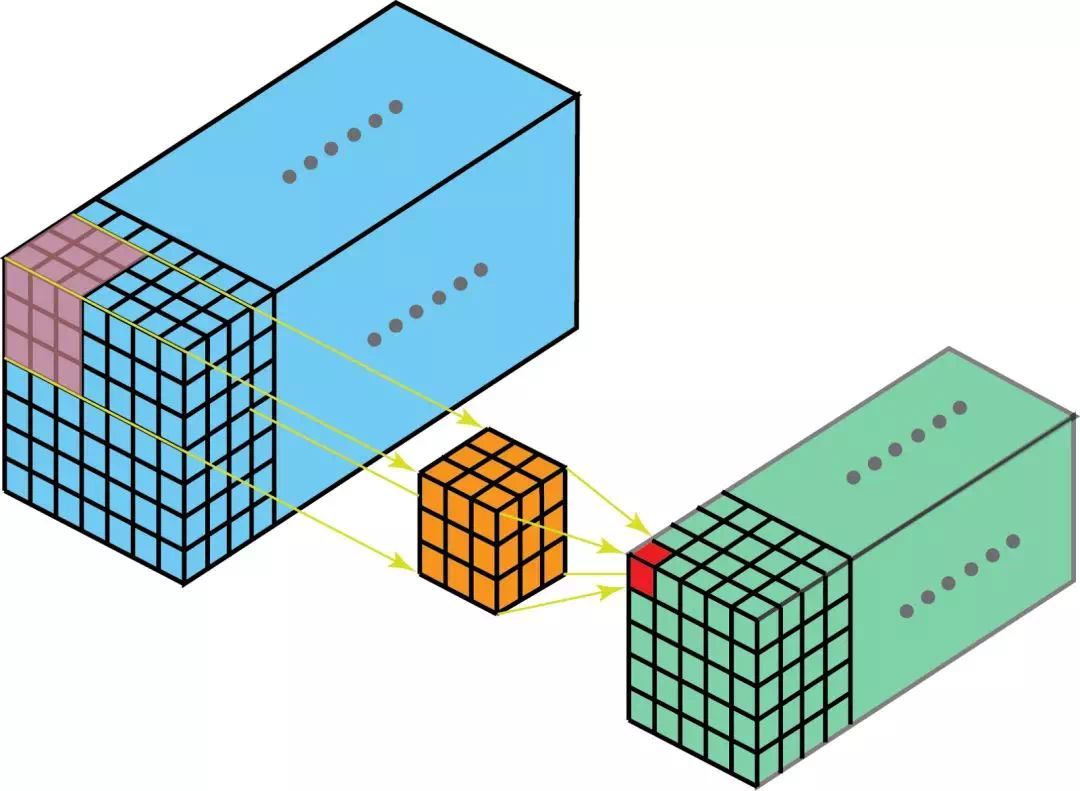
在多通道卷积中,filter 的每个 kernel 在对应的 channel 上进行运算,得到 n 个中间输出结果,将这 n 个中间输出结果进行相加,得到一个单一通道的输出,这个单一通道的输出就是一个滤波器在 layer 中的输出结果。
例如输入是一个 5*5*3 的矩阵,filter 是一个 3*3*3 的矩阵。首先,filter 中的每个 kernel 分别应用于对应的 channel 中,执行三次卷积,得到 3 个 3*3 的特征图。
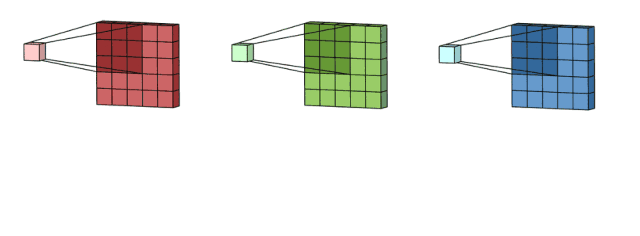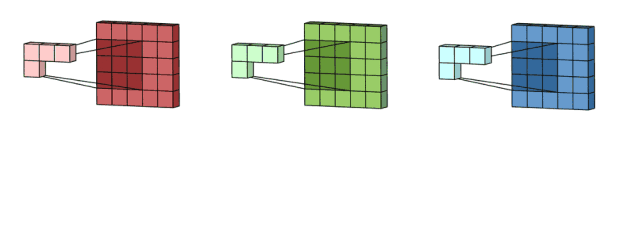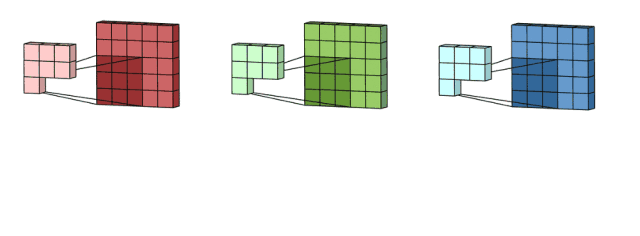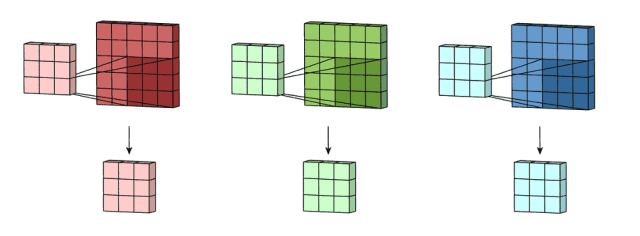
然后,这三个通道相加(矩阵加法),得到一个 3*3*1 的单通道。这个通道就是在输入层(5*5*3 矩阵)应用 filter 的结果。
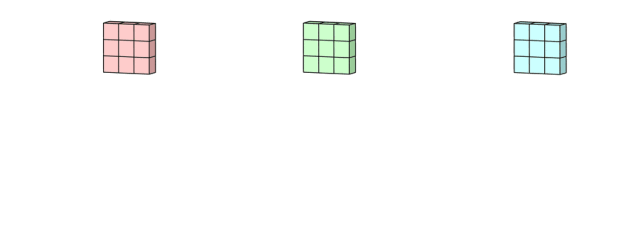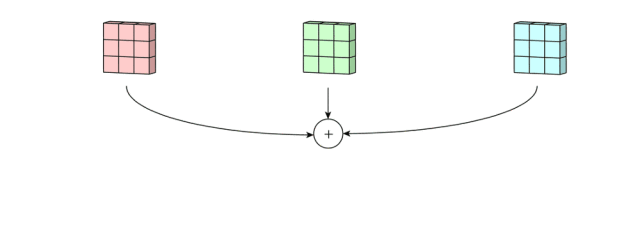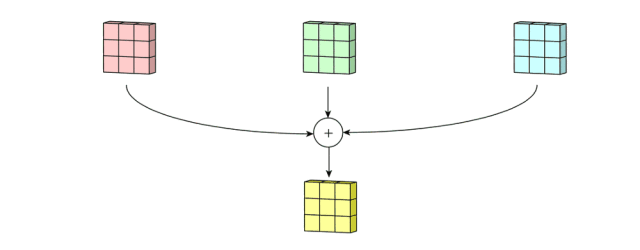
将图形转换成 3D 层面来看,就是一个 3D filter 的滑动过程,输入层和 filter 有相同的深度(channel 数量 = kernel 数量)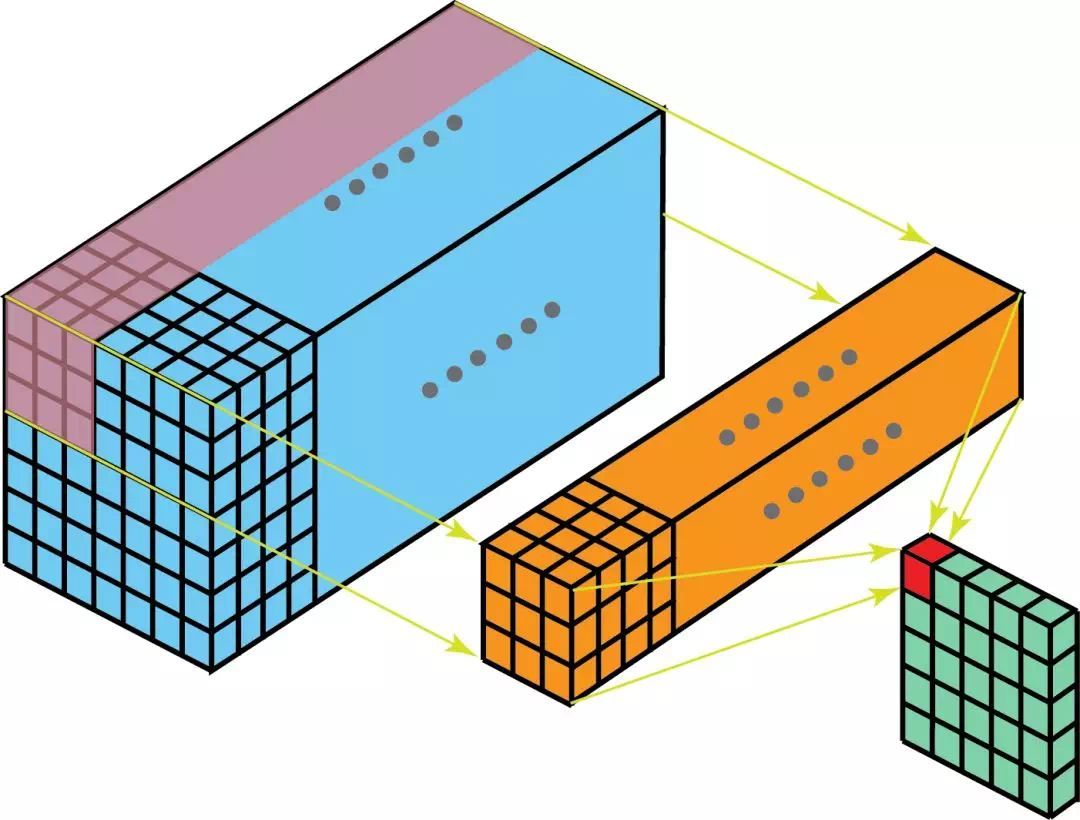
接下来,来看通过卷积操作进行层与层之间深度的转换。假设输入层有 个通道,我们想得到 个通道。由上面内容可知,每个 filter 得到的输出都是一个单通道的结果,想要得到有 个通道的输出结果,我们只需要使用 个 filter。即有 个 filter,每个 filter 有 个 kernel,完成卷积后将结果堆叠在一起,即得到输出层。
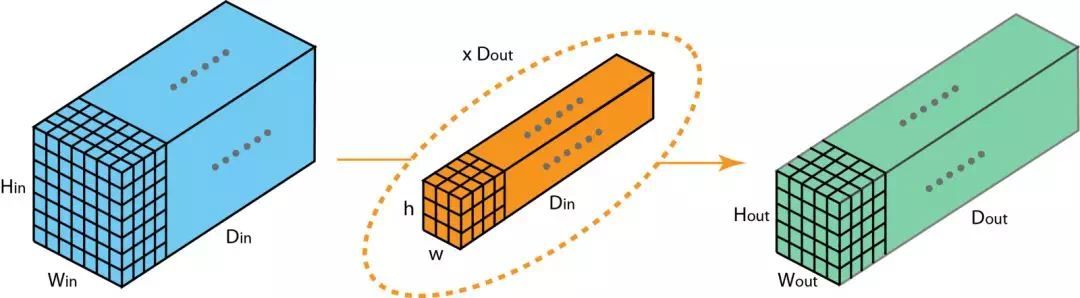
虽然这里的卷积是 3D 的,但是因为 filter 的 kernel 数和 layer 的 channel 数相同,所以在深度方向卷积核不进行滑动,只在宽和高方向进行移动,单个 filter 得到的输出也是 2D 的,所以仍称为 2D 卷积
3D 卷积
3D 卷积相比上述 2D 卷积,则是在深度方向也进行滑动,即 filter 的 kernel 数要小于输入层的深度,所以 filter 需要在数据的三个维度上进行滑动,单个 filter 得到的结果也是 3D 的。